Astrodynamics
What, how and why?
Astrodynamics is the analysis of the motion of natural and artificial objects in space, subject to environmental and artificial forces.
This area has been in constant evolution due to the constant emergence of new technologies, such as Low-Thrust Systems and solar radiation induced propulsion, and brand new theoretical techniques, like topological manifolds and deep learning.
Practical Experience
I have worked with three excellent researchers in the field of Astrodynamics: Sylvio Ferraz-Mello, Helio K. Kuga and Antontio Bertachini Prado.
Orbit prediction for Brazilian satellites
My project with Dr. Helio Kuga (National Institute for Space Research) aimed at coding methods of preliminary orbit determination in order to qualify them using real data from Brazilian satellites and analyze their numerical performance. I learnt a lot on the basics of Astrodynamics in the process and coded, in Fortran 90, the Gibbs and Gauss methods for orbit determination. These methods take, respectively, three and two position vectors of a spacecraft and use the time between their passage to predict the entire orbit.
I have also worked with satellite orbit integration using Python programming during a few graduate courses. You can find my codes for Orbital Movement of Satellites, Spacecraft Dynamics & Control and Periodic Orbits in my Github page.
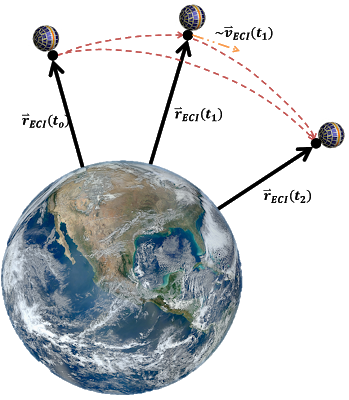
Gibbs method illustration (Source).
Low Thrust Orbit Optimization and Radiation Exposure
The goal of my work with Dr. Antonio Prado (National Institute for Space Research) was to measure the amount of radiation a spacecraft receives once it leaves the sphere of influence of Earth in a Low Thrust Orbit (LTO). The spacecraft crosses the Van Allen belts many times during the transfer, in which particles such as protons and electrons can damage the onboard electronic equipment. I developed a mathematical model for the density of particles of the belt in space, as can be seen in the figure below, making it possible to integrate the flux of particles in time and compute the total dose of radiation absorbed by the spacecraft according to the chosen trajectory.
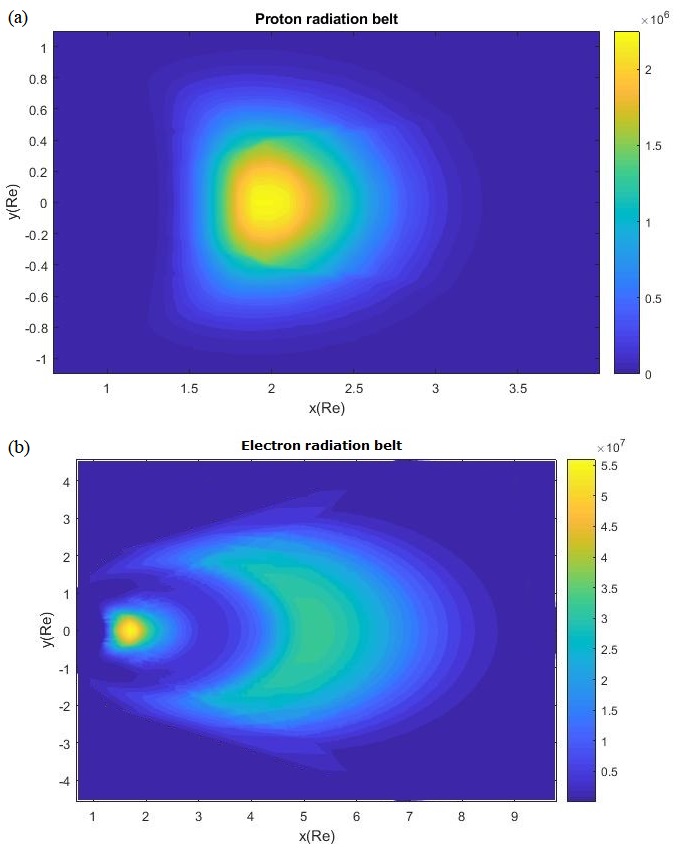
Contour map model for the flux of: a) protons, b) electrons in the Van Allen Belts; Re = 6378 km.
Then, I incorporated a model for the Moon inclination variation at the time of the transfer. Since the Earth's axis changes with time, as well as the relative inclination of the Moon's orbit, it is important to be able to exploit this in order to choose orbits that pass through the less concentrated parts of the Van Allen Belts.
Inclination of the lunar orbit with respect to the Earth‘s equator according to the considered date. (R. B. Roncoli, 2005)
Finally, different trajectories were computed, varying in initial eccentricity, initial height, transfer date (proxy for the initial Moon orbit inclination) and type of propulsion system, which gave the following final parameters of interest: mission duration, fuel consumption, time in Van Allen belts and fluence of protons and electrons absorbed. Using an optimization algorithm, thousands of trajectories were tested and the best ones with respect to the final parameters can be seen in the plots below.
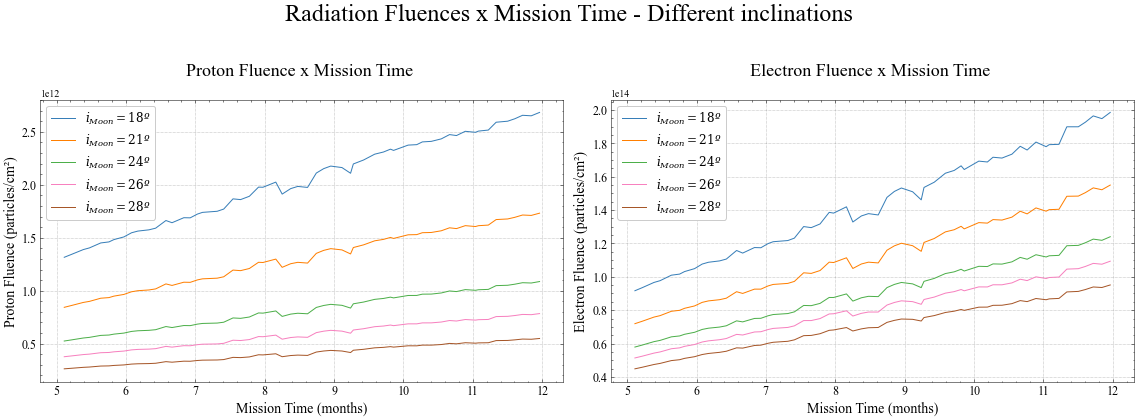
Fluence of particles as a function of mission time for a myriad of inclinations of the Moon in respect to the Earth's orbit.
Academic Background
AME 30381 - Orbital & Space Dynamics
AGA0504 - Classical Mechanics
AGA0502 - Planets and Planetary Systems
PTC3572 - Dynamics and Control in Discrete Time
PTC3313 - Control Systems
4302306 - Mechanics II
CMC-020 - Introduction to Orbital Mechanics
CMC-303-4 - Artificial Satellites - Orbital Movement
CMC-411-4 - Periodic and Quasi-Periodic Orbits in the Three Body Problem
Prof. Flint Thomas - University of Notre Dame (45 hours)
a) Dynamics of point masses: Time derivatives of moving vectors, Fixed and moving frames of reference, Relative motion, Newton's second law of motion; b) n-body, three-body and two-body problems: Analytical solution of the equations of motion for the two-body problem, Numerical solutions of equation of motion, Equation of relative motion, Angular momentum and orbit formulas, The energy law, Libration points (Lagrange points); c) Orbital position as function of time: Eccentric anomaly, Circular, ellipsoidal, parabolic and hyperbolic trajectories, Universal variables; d) Orbit in space: Orbital elements and state vectors, Coordinate transformations, Geocentric and perifocal frames, Ground tracks; e) Preliminary orbit determination: Topocentric coordinate systems, Lambert's problem, Sidereal time, Orbit determination; f) Orbital maneuvers: Impulsive orbit transfers, Hohmann transfer, Chase maneuvers, Non-impulsive orbital maneuvers; g) Relative motion and rendezvous: Conditions of interceptions and rendezvous, Linear orbit theory, Clohessy-Wiltshire equations; h) Interplanetary mission analysis: Interplanetary Hohmann transfers, Sphere of influence, Method of patched conics, Planetary departures, rendezvous and flyby; i) Satellite attitude dynamics: Torque-free motion and its stability, Dual-spin spacecraft, Attitude control thrusters, Yo-yo despin mechanism, Gyroscopic attitude control.
Prof. Tatiana Michtchenko - University of São Paulo (60 hours)
Newton's laws, equations of motion of a particle. Conservation of momentum and energy. Harmonic oscillator. Central forces, Newtonian gravitation. Gravitational potential, escape velocity. 2-body problem. Kepler's laws and Rutherford scattering. Orbit determination. Introduction to the N-body system. Movement in non-inertial references. Balance, Lagrange points. Virial Theorem. Lagrangian formalism. Introduction to Hamilton's theory. Introduction to rigid bodies and precession of the Earth.
Prof. Jane Hetem - University of São Paulo (60 hours)
1) The Celestial sphere; 2) Dynamics and movement of the planets; 3) Origin and structure; 4) Compared planetology; 5) terrestrial planets; 6) Giant planets; 7) Planetary magnetospheres and the interplanetary medium; 8) Planetary atmospheres; 9) Planetary surfaces; 10) Planetary interiors; 11) Small bodies; 12) Transnetunian objects; 13) Formation of planets and planetary systems; 14) extrasolar planets; 15) The Sun
Prof. Luiz H. A. Monteiro- University of São Paulo (60 hours)
1. Introduction. 2. State space. 3. Discrete-time linear dynamical systems: analytical solution. 4. Lyapunov stability: indirect and direct methods. 5. Discrete-time nonlinear dynamical systems: fixed point and periodic orbit. 6. Hartman-Grobman Theorem. 7. Bifurcations. 8. Comparisons with the continuous-time system theory. 9. Chaos. 10. Applications.
Prof. Fuad K. Júnior - University of São Paulo (60 hours)
Fundamentals. Open-loop and closed-loop control. General scheme of a feedback system. Modeling of physical systems. Analysis of transient response. Design specifications in the time-domain. Stability. Routh-Hurwitz criterion. Steady-state error analysis. Root Locus Method. Frequency response methods. Nyquist criterion. Minimum-phase systems. Stability margins. Frequency response of closed-loop systems. Cutoff frequency and bandwidth. Relationship between step response and frequency response. Design techniques and compensation.
Prof. Arnaldo Gammal - University of São Paulo (60 hours)
1. Rigid Body, Angular Momentum and Kinetic Energy.
2. Tensor of Inertia, main axes of inertia. Euler angles. Euler's equations of motion for a rigid body. Rotation around a fixed axis. The symmetrical top.
3. Canonical transformations.
4. Hamilton-Jacobi theory. Angle-action variables.
Profs. Evandro Marconi Rocco & Valdemir Carrara - National Institute for Space Research (60 hours)
Central field. Newton's laws. Universal law of gravitation. Central force. Integral of angular momentum. Areolar speed. Trajectories of movement. Integral energy. Binet equation. Kepler's laws. Ellipse properties. Problem of the two bodies. Reduction of the problem of two bodies. Solution of the problem of the two bodies. Elliptical movement. Cartesian coordinates of the plane movement. Satellite positioning. Keplerian elements. Coordinate transformation. Obtaining the state vector. Inverse problem. Coordinate systems. Horizontal coordinates, hourly coordinates, equatorial coordinates. Topocentric system, geodetic coordinates. Time systems. Introduction to orbit determination. Earth's gravitational potential.
Profs. Renato & Marcelo Lopes - National Institute for Space Research (60 hours)
Review of Laplace transform. Mathematical models of physical systems: transfer functions, block diagrams, obtaining transfer functions from physical systems. Analysis of the response in time: impulsive response, first order systems, second order systems, higher order systems, Routh's stability criterion, analog computers. Notions of the locus of roots. Frequency response methods: logarithmic graphs, Bode diagrams. Introduction to modern control: state variables, transition matrix, etc.
Profs. Valeri Vlassov & Rafael Lopes Costa - National Institute for Space Research (60 hours)
Conduction heat transfer, Fourier's law. Natural and forced convection. Heat transfer by radiation; Planck, Wien, Stefan-Boltzmann laws. Form and Gebhart factors, radioactive couplings.
Heat transfer in electronic components and satellite elements. Permanent, transient, regular and periodic regimes. Balance in thermal networks. Differential equations of the nodal method. Closed-loop temperature control. Thermal mathematical models of PID and NO-OFF controllers.
Orbital heat flows. Thermal characterization of orbits; beta angle. Absorbency and emissivity (two-band model), thermal coatings. MLI super-insulating radiators and blankets. Heat pipes and other thermal control devices. Satellite thermal balance.
Prof. Antônio Bertachini Prado - National Institute for Space Research (60 hours)
Terrestrial gravitational field. Expression for geopotential. Representation of
spherical harmonics. Numerical formulas for calculating the geopotential. Forces
disturbing. Gravitational force due to the potential of the body. Attraction
gravitational force of the Sun and Moon. Drag force. Tidal forces due to the Moon and
Sun. Radiation pressure force. Albedo. Analytical methods of disturbance.
Brouwer methods. Von Zeipel's method. Numerical methods of perturbation.
Integration of motion equations. Time transformations. Model
unified state. Semi-analytical methods of disturbance. Solution methods.
Averaging method.
Prof. Antônio Bertachini Prado - National Institute for Space Research (60 hours)
Elements of Ordinary Differential Equations: First and Second Systems
Order, Linearization and Equilibrium Points, General Solution of the Linear System,
Breakeven Point Classification, Phase Diagrams, Transition Between Types of
Equilibrium, Nonlinear Systems: Solution Stability, Equations with
Periodic Coefficients: Floquet Theory, Monoparametric Families of Orbits
Periodic, Analytical Continuation Method.
Basic Notions of Disturbance Theory: Media Methods, LindstedtPoincaré Method, Multiple Time Scales Method.
Bifurcation Theory Concepts: Linear Theory in Flows and Maps, Theory No
Linear, Normal Forms and Hamiltonian Systems, Poincaré-Birkhoff Theorem,
Saddle-Node Bifurcations, Transcript, Pitchfork and Hopf, Reduction to Variety
Central.
The Restricted Three-Body Problem: The Circular Problem vs. Elliptical, Points
Liberation and its Disturbances, Models and Equations of Motion, Orbits
Periodicals: Families from Copenhagen, Hénon, etc. Orbits Around Points
Balance.
Halo and Lissajous Orbits: Existence of Solutions, Determination of Orbits:
Numerical and Analytical Methods, Lindstedt-Poincaré Method and Continuation
Analytics, Halo Orbite Families, Resonances, Control and Maintenance of
Orbits, Transfer between Orbits of the Same Family.
Prof. Hanspeter Schaub - University of Colorado at Boulder (on Coursera) (~28 hours)
The movement of bodies in space (like spacecraft, satellites, and space stations) must be predicted and controlled with precision in order to ensure safety and efficacy. Kinematics is a field that develops descriptions and predictions of the motion of these bodies in 3D space. This course in Kinematics covers four major topic areas: an introduction to particle kinematics, a deep dive into rigid body kinematics in two parts (starting with classic descriptions of motion using the directional cosine matrix and Euler angles, and concluding with a review of modern descriptors like quaternions and Classical and Modified Rodrigues parameters). The course ends with a look at static attitude determination, using modern algorithms to predict and execute relative orientations of bodies in space.
Prof. Hanspeter Schaub - University of Colorado at Boulder (on Coursera) (~21 hours)
As they tumble through space, objects like spacecraft move in dynamical ways. Understanding and predicting the equations that represent that motion is critical to the safety and efficacy of spacecraft mission development. Kinetics: Modeling the Motions of Spacecraft trains your skills in topics like rigid body angular momentum and kinetic energy expression shown in a coordinate frame agnostic manner, single and dual rigid body systems tumbling without the forces of external torque, how differential gravity across a rigid body is approximated to the first order to study disturbances in both the attitude and orbital motion, and how these systems change when general momentum exchange devices are introduced.
Prof. Hanspeter Schaub - University of Colorado at Boulder (on Coursera) (~31 hours)
This course trains you in the skills needed to program specific orientation and achieve precise aiming goals for spacecraft moving through three dimensional space. First, we cover stability definitions of nonlinear dynamical systems, covering the difference between local and global stability. We then analyze and apply Lyapunov's Direct Method to prove these stability properties, and develop a nonlinear 3-axis attitude pointing control law using Lyapunov theory. Finally, we look at alternate feedback control laws and closed loop dynamics.
Prof. Hanspeter Schaub - University of Colorado at Boulder (on Coursera) (~44 hours)
The goal of this capstone spacecraft dynamics project is to employ the skills developed in the rigid body Kinematics, Kinetics and Control courses. An exciting two-spacecraft mission to Mars is considered where a primary mother craft is in communication with a daughter vehicle in another orbit. The challenges include determining the kinematics of the orbit frame and several desired reference frames, numerically simulating the attitude dynamics of the spacecraft in orbit, and implementing a feedback control that then drives different spacecraft body frames to a range of mission modes including sun pointing for power generation, nadir pointing for science gathering, mother spacecraft pointing for communication and data transfer. Finally, an integrated mission simulation is developed that implements these attitude modes and explores the resulting autonomous closed-loop performance.
